# Oldschool
See original writeup and challenge files [here](https://github.com/xrmon/ctf-writeups/tree/master/2019/confidence-ctf)

For this challenge we were given an MSDOS executable, oldschool.exe, and a text file flag.txt containing a weird jumble of characters in UTF-16. We use dos2unix to convert it into unix-friendly
UTF-8, with ‘\n’-style newlines:
```
$ dos2unix flag.txt
dos2unix: converting file flag.txt to Unix format ...
$ cat flag.txt
4 {4pp
p {k4{ E
p 44p{ p
4 p
S

$
```

Opening up the file with radare, we notice some interesting quirks about how DOS works. Instead of calling library functions (puts, printf…), the program makes calls to the DOS API by setting
registers accordingly and using the **int 0x21** instruction. We can read about the DOS API here: http://spike.scu.edu.au/~barry/interrupts.html

The first API interrupt in the file sets AH to 9, indicating “write string to stdout”. This prints the string in DX, which is “Give me a flag to draw!” - so the weird arty text file above must be
the output of this program with the flag! Interestingly, strings in DOS are ‘$’-terminated instead of NULL terminated like we would normally expect.


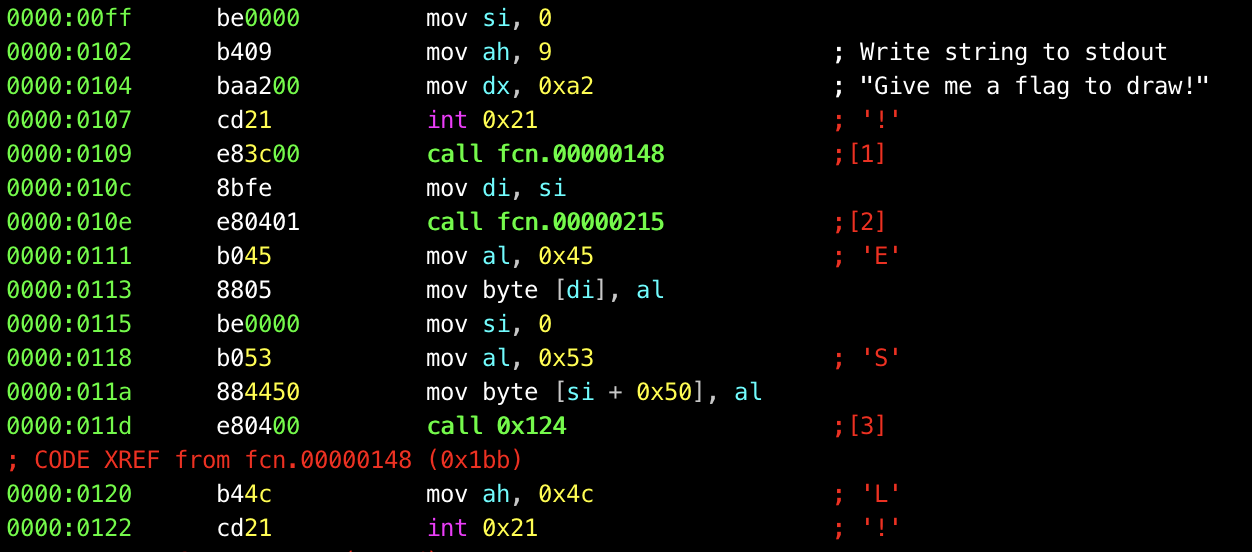
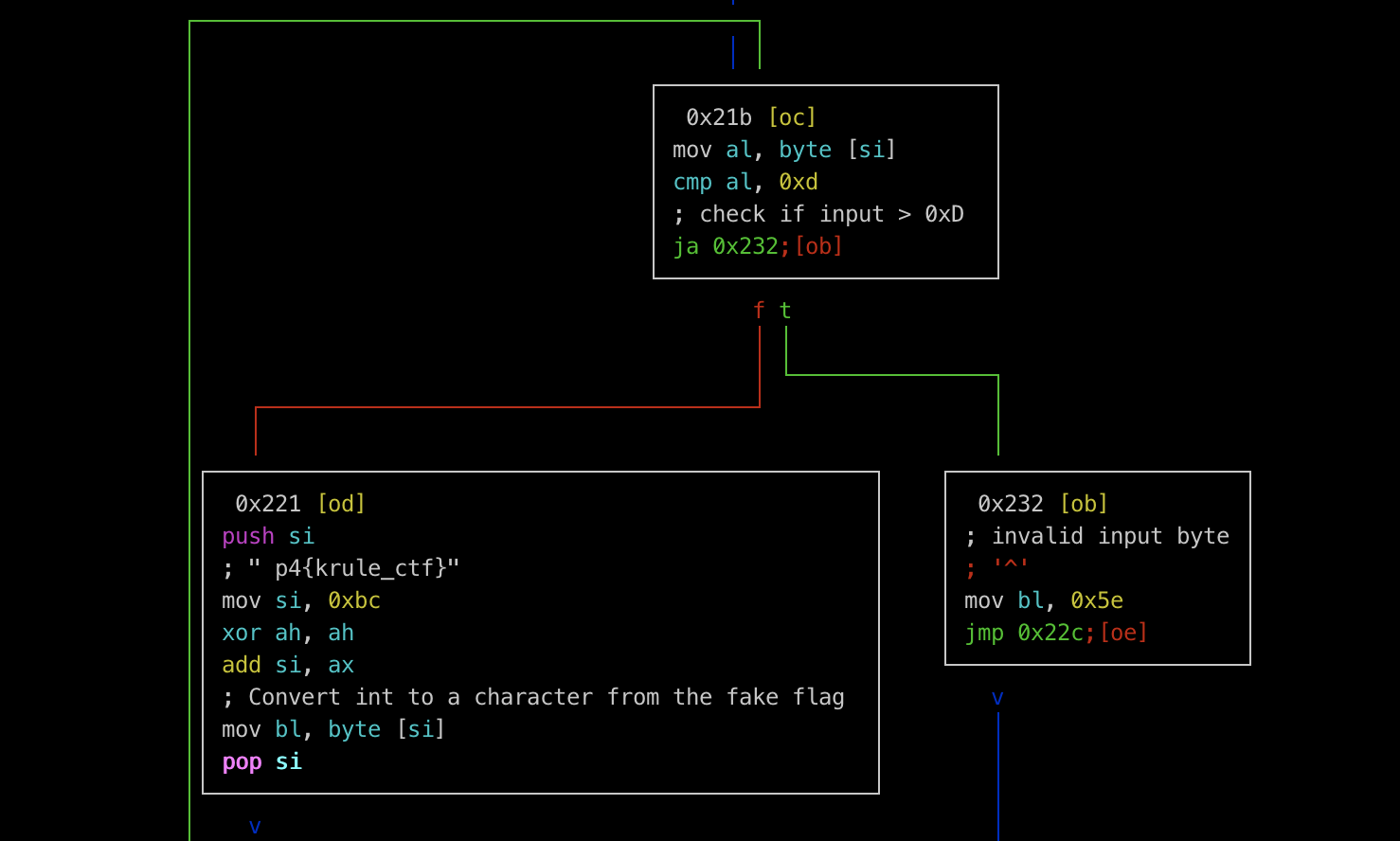
As we can see, there are three main functions called from this program. The first looks a horrific mess of basic blocks, which continues for several pages of scrolling through Radare’s graph view
(accessible when in a function by typing VV). The second is a simple for loop an array of size 0xA2, which was presumably produced from the horrific first function. There is a fake flag, “
p4{krule_ctf}” stored at address 0xBC.

For each byte in the array, it uses the byte’s value as a position in the fake flag to produce a single character, which we store back in the array - this must be how the flag’s drawing was
produced! If the value in the array is greater than the length of the fake flag, we simply write a ‘^’ character. We don’t see this in flag.txt, so we know this didn’t happen.


The third and final function is fairly boring, it simply adds newlines every 18 characters, giving 9 lines of output (0xA2 / 18 = 9). The only slightly interesting thing here was that since the
program exits by a call to the DOS API, there is no ret instruction in the entry function, meaning radare tried to analyse this third function as part of the entry function (since it was the next
thing in memory). I decided not to waste time figuring out the commands to manually fix it, since I knew what the function did anyway.

The first function was by far the most time consuming part of the challenge. The first section was relatively easy to reverse: it takes a byte of hex as input and converts it to an integer. Then,
there is a for loop with four iterations: It does a thing with the lowest bit of the input byte, then does a thing with the second lowest bit, then finally it bit shifts right by two so that the
next iteration operates on the next bits. The operation looks something like:
```
hex = input()
byte = int(hex)
for i in range(0, 4):
do_thing_with_first_bit(byte)
do_thing_with_second_bit(byte)
byte = byte >> 2
```

This entire operation is wrapped in yet another for loop, this time with 9 iterations. So, overall, the user gives 9 bytes of input to the program. We now know that the flag is 9 bytes long! Upon
closer inspection and after a few hours of reversing, we discovered the purpose of the two functions which operate on each bit of the input. Remember that array of size 0xA2 that we process in the
second and third functions? Well, turns out we keep track of a position in that array, and move that position on each iteration of the inner for loop. After each iteration, we increment our
position by 1, producing the array of lowish values which eventually gets printed out in an artsy fashion.

The two functions which operate on the first and second bit for each iteration actually just move the position left or right, and up or down in the array. The logic looks complicated and scary
because the program checks if we would go off the edge of the array, and stays put if so. But with that caveat it’s a relatively simple function. In pythonic pseudocode, the overall logic now
looks like:
```
pox = 0x50
for i in range(0, 9):
hex = input()
byte = int(hex)
for j in range(0, 4):
pos = first_thing(byte, pos)
pos = second_thing(byte, pos)
byte = byte >> 2
array[pos] += 1
```

Where the functions first_thing and second_thing move the position left, right, up and down as such:
```
def first_thing(byte, pos):
bit = first_bit(byte)
if bit == 1 and not at edge of array:
# Move right
pos += 1
elif bit == 0 and not at edge of array:
# Move left
pos -= 1
else:
# Keep position the same
return pos

def second_thing(byte, pos):
bit = second_bit(byte)
if bit == 1 and not at edge of array:
# Move down (each row is length 18)
pos += 18
elif bit == 0 and not at edge of array:
# Move up (each row is length 18)
pos -= 18
else:
# Keep position the same
return pos
```

In addition, we are given the starting position 0x50, hardcoded into the binary and marked with an ’S’ into the program output. The final position is also given, marked with an ‘E’. We now have
the task of finding a path through the grid from S to E, which increments each position in the array the correct number of times. There’s probably a clever algorithm for doing stuff like this, but
for smallish problems like this I like to sit down and have a go by hand since it’s often quicker than finding and developing the algorithm for it.

A while later sat drawing and redrawing solutions on a whiteboard, I came up with a solution which worked:

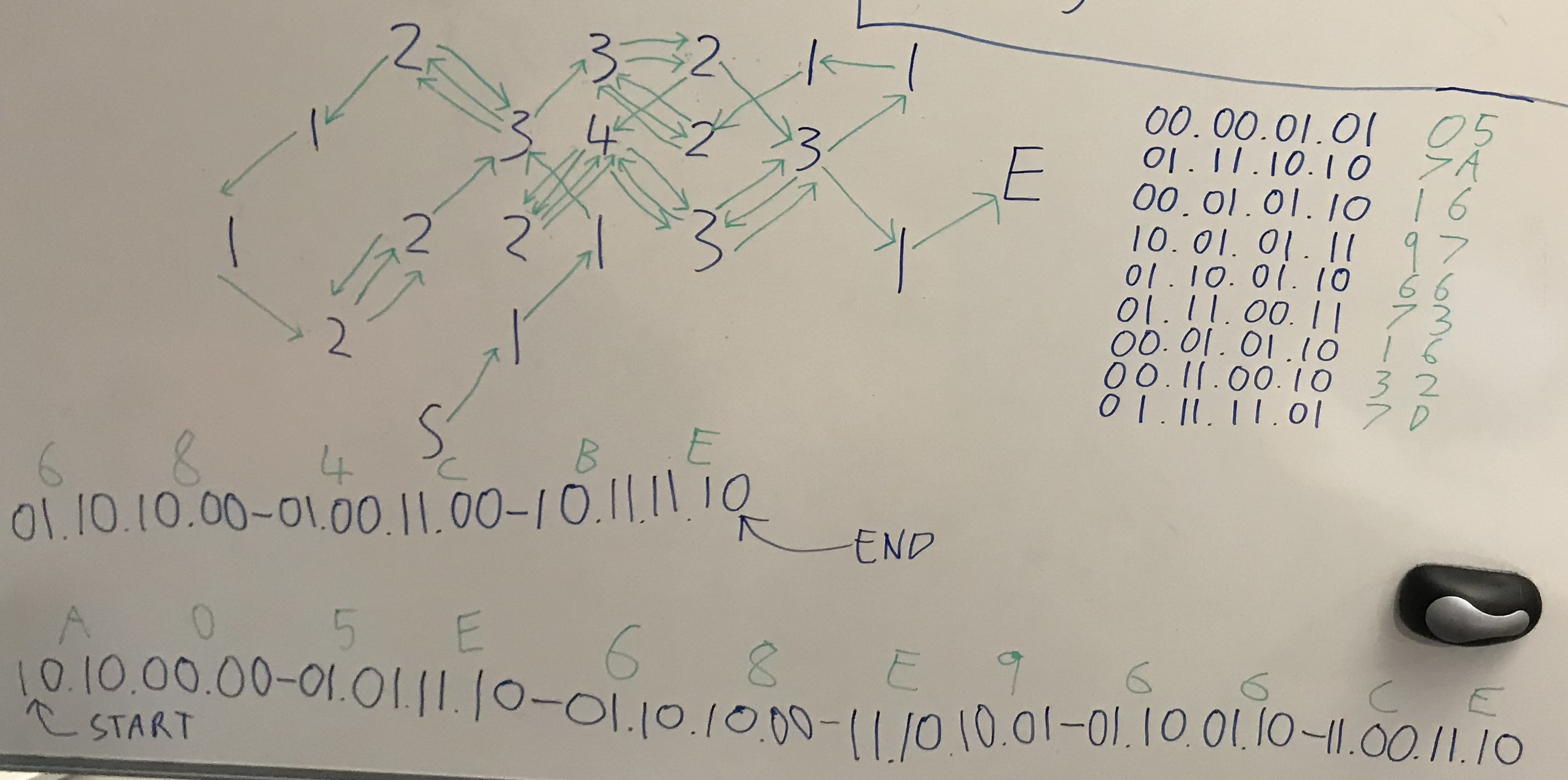
Writing out this solution in terms of bits, converting to hex and remembering to reverse the bits in each byte so they are processed in the right order, this gave us the following solution:
057a1697667316327d

After adding the ‘p4{‘ and ‘}’ required by the flag format, I submitted this to the scoring system, and… was greeted by a “wrong flag” message.

At this point I downloaded dosbox from dosbox.com and emulated the program with my input, and sure enough, it printed exactly the same output that we were given. After verifying this I contacted
an admin on IRC who was very friendly and gave me a hint towards finding the solution: I had ignored the ‘p4{‘ & ‘}’ strings from my answer since they were not valid hex characters and would be
rejected by the program. However, these are a necessary part of the solution. It turns out the program actually takes the hex encoding of the flag, meaning the program input is something like
70347b??????????7d (since we know the flag starts with ‘p4{‘ and ends with ‘}’).

This actually makes the problem significantly easier, since we are given part of the route already and must simply find the rest of it (remember, each pair of bits in the solution gives us a move
left/right, and a move up/down, meaning every move is diagonal unless we are at the edge of the array). With the new fixed parts of the route that we have discovered marked in red, and arrows I
added marked in green, this now gives us:

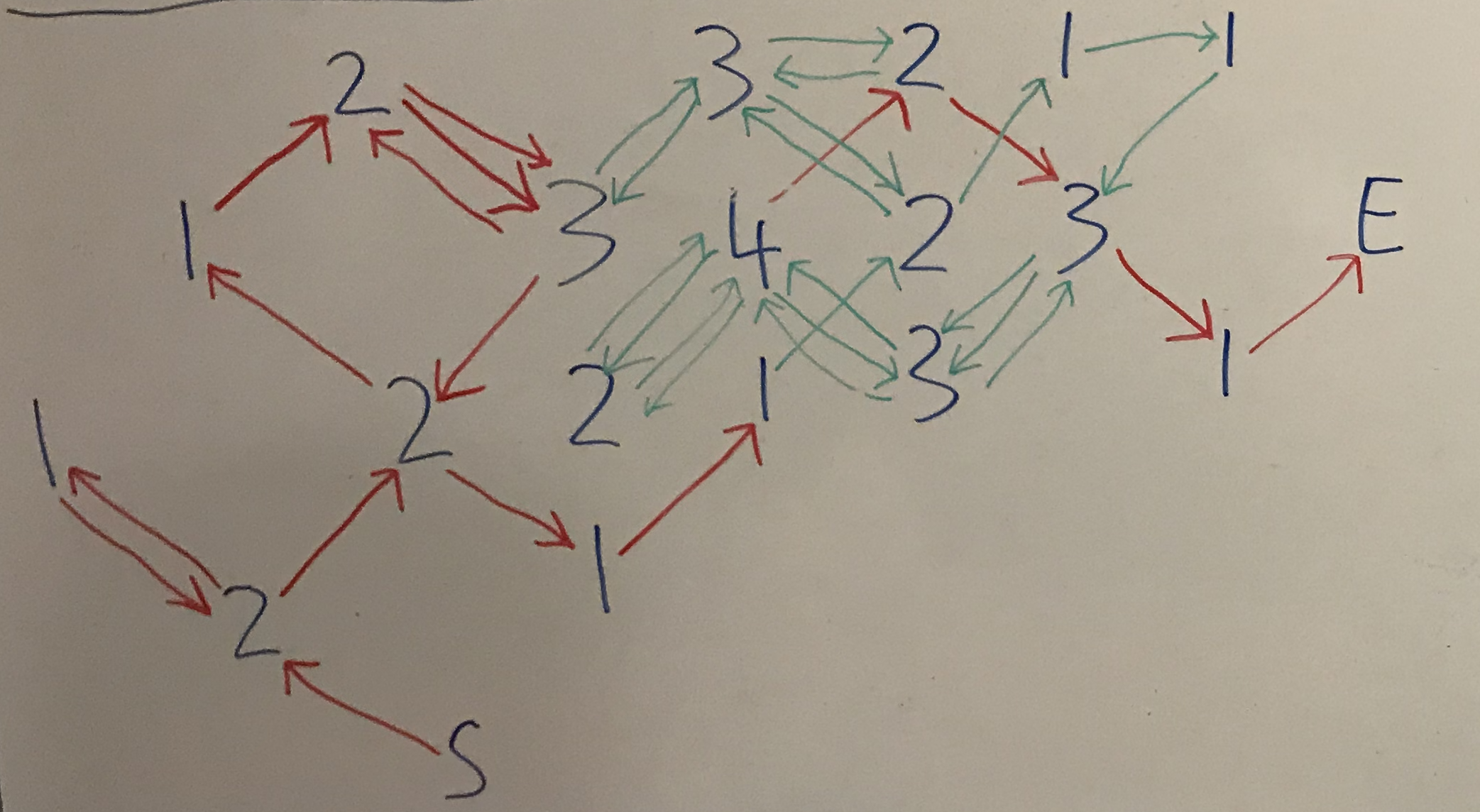
Converted to hex, we now get, 70347b61716932667d, which when decoded gives us p4{aqi2f}, which is the actual flag for the challenge.