Rating:
# Mine the gap
You are given a script `minesweeper.py`, and a text file, `gameboard.txt`. Invoking the python script requires `pygame` to be installed.
pip install pygame
It takes several seconds to load. After loading, we get a minesweeper game
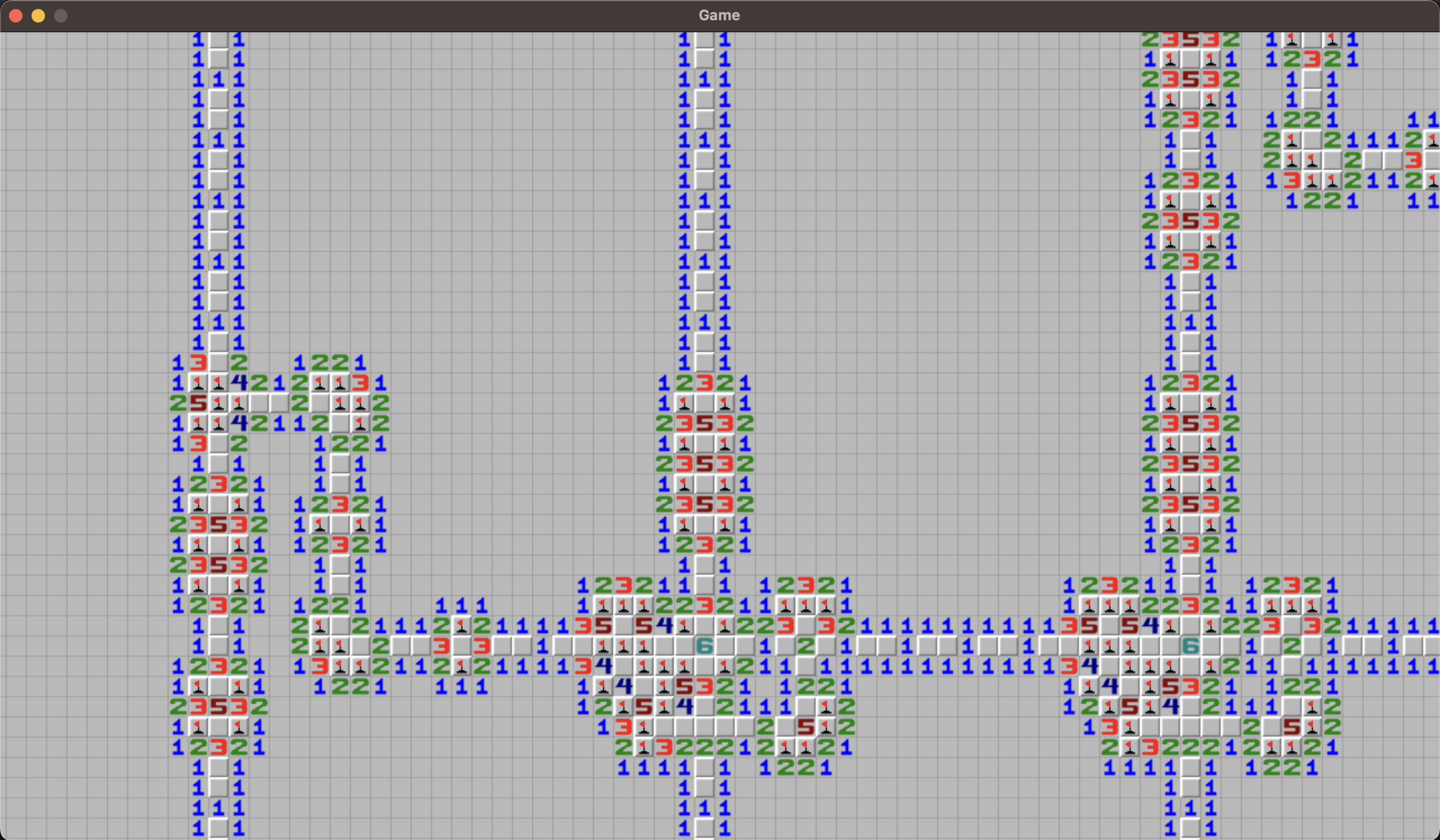
Inspect the script and search for CTF / FLAG etc.
We see this part of the code:
```python
if len(violations) == 0:
bits = []
for x in range(GRID_WIDTH):
bit = 1 if validate_grid[23][x].state in [10, 11] else 0
bits.append(bit)
flag = hashlib.sha256(bytes(bits)).hexdigest()
print(f'Flag: CTF{{{flag}}}')
else:
print(violations)
```
We need to solve it, and then we can reconstruct the flag from the solution.
Inspect `gameboard.txt` -- it looks like the board is in a simple text format.
The board looks pretty structured. Putting one mine will collapse many other cells, but not all.
```bash
❯ wc gameboard.txt
1631 198991 5876831 gameboard.txt
```
The board is 1600 x 3600 cells. It is huge. It is not possible to solve it by hand.
We need to solve the board with code.
Idea 1 use backtracking and pray to be fast enough.
Idea 2 skip backtracking and use SAT solver (Z3). This is what we did.
With Z3, we can create variables and constraints on the values they can get, then ask for a solution. If there is a solution, Z3 will give us the values for the variables. Z3 will find an answer in a reasonable™️ time.
Check the code to generate the solution. With the answer, we can easily recover the flag using the game's code.
```python
import z3
with open('gameboard.txt') as f:
data = f.read().split('\n')
rows = len(data)
cols = len(data[0])
print(rows, cols, flush=True)
solver = z3.Solver()
vars = {}
def get_var(i, j):
assert data[i][j] == '9'
if (i, j) not in vars:
vars[i, j] = z3.Int(f'var_{i}_{j}')
solver.add(0 <= vars[i, j])
solver.add(vars[i, j] <= 1)
return vars[i, j]
for i in range(rows):
for j in range(cols):
if data[i][j] in '12345678':
flags_on = 0
pending = []
for dx in [-1, 0, 1]:
for dy in [-1, 0, 1]:
if dx == 0 and dy == 0:
continue
nx = i + dx
ny = j + dy
if 0 <= nx < rows and 0 <= ny < cols:
if data[nx][ny] == 'B':
flags_on += 1
elif data[nx][ny] == '9':
pending.append(get_var(nx, ny))
if not pending:
continue
solver.add(z3.Sum(pending) + flags_on == int(data[i][j]))
print(len(vars))
for i in range(rows):
for j in range(cols):
if data[i][j] == '9':
assert (i, j) in vars
print("Solving...")
print(solver.check())
for (i, j), v in vars.items():
if solver.model()[v] == 1:
print(i, j)
```