Let's approach this problem by modelling each hacker and the flow of their virus as a node and an edge respectively in a directed graph. Knowing that each hacker can transmit their virus to only one other hacker, the number of possible graph structures is only three. One of them is shown below.


Here, the nodes 3, 4, 5, and 6 are in a "deadlock", and any virus transmitted by one of these nodes pass through that node again. To find cycles like this, the idea is simple: Start at any node and keep traversing along the node it points to, adding each node to an array, say, visited. If at any point, the next node is already in visited, then we have detected a cycle beginning and ending at that node.

To keep track of the nodes that are in a cycle, we'll need two sets, say, good_nodes and deadlocked_nodes, to store the nodes not in a cycle and the nodes in a cycle respectively. We'll then split visited at the node that starts the cycle: Every node to the left of the split goes in to good_nodes and every node to the right of the split (inclusive) goes in to deadlocked_nodes. In our example, by the time we have traversed 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 3, we will see that node 3 is already in visited, so we split at node 3, so that good_nodes will be {1, 2} and deadlocked_nodes will be {3, 4, 5, 6}.

The other structures could be the following.


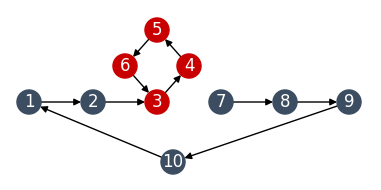
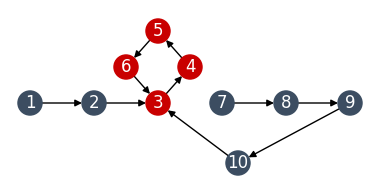
Here, node 10 points to a node that is either not in a cycle (ie., in good_nodes) or in one (ie., in deadlocked_nodes). In either case, it is easy to see that the nodes from 7 through to 10 will not be in a cycle. If we ever come across a path like this, we simply add all the visited nodes to good_nodes.

Now that we know the edge cases, it is straightforward to write the following linear-time function to find cycles ([Here's](https://github.com/gov-ind/ctf_solves/raw/main/2022/hsctf/hacking/solve.py) the full solve script).

```
def find_num_deadlocked_nodes(test):
good_nodes = set()
deadlocked_nodes = set()

for idx, target in enumerate(test):
if idx in good_nodes:
good_nodes.add(idx)
continue

visited = [idx]
next_idx = target - 1

while True:
if next_idx in good_nodes or next_idx in deadlocked_nodes:
good_nodes |= set(visited)
break

if next_idx in visited:
good_nodes |= set(visited)

split_idx = visited.index(next_idx)
_deadlocked_nodes = set(visited[split_idx:])

deadlocked_nodes |= _deadlocked_nodes

break

visited.append(next_idx)
next_idx = test[next_idx] - 1

return len(deadlocked_nodes)
```

Original writeup (https://gov-ind.github.io/hsctf_2022).