Original Writeup: [https://gov-ind.github.io/hsctf_2022](https://github.com/gov-ind/ctf_solves/raw/main/2022/hsctf/tunnels/solve.py)

Let's first look at a simpler version of the problem where there are only 4 houses in a row. Here it seems intuitive that guessing either 2 or 3 over four rounds will catch the robber with a high probability.

Let's recap what this probability is: The probability that we make a correct guess 4 rounds is 1 minus the probability that we don't make a correct guess each round. If we let $\overline{X}$ to be the event that we do not make a correct guess over four rounds, $P(\overline{X}; [h_1, h_2, h_3, h_4])$ to be the probability that we don't make a correct guess over four rounds with $h_1, h_2, h_3, h_4$ as our guesses, and $P_n(\overline{X}; h_n)$ to be the probability that we don't make a correct guess in round $n$ with a guess of $h_n$, then, for a sequence of guesses 2, 2, 3, 3, we have:

$P(X;[2,2,3,3]) =1−P(\overline{X};[2,2,3,3]) = 1−P_1(\overline{X}; 2) \cdot P_2(\overline{X}; 2) \cdot P_3(\overline{X}; 3) \cdot P_4(\overline{X}; 4)$

Let's walk through this example so that the formula makes more sense. In round 1, the robber could be in any one of four houses, so we might as well guess any house. Let's say we guess house 2 so that $P_1(\overline{X}, 2) = \frac{3}{4}$ (in other words, there's a 75% chance we are wrong). Now there are two possibilities: Either our guess was correct, in which case we are done with this round, or we are wrong, in which case the robber will be in an adjacent house in the next round.

More concretely, if the robber were actually in house 1, there's a 100% chance he's now in house 2. If he were in house 3, there's a 50% chance he's now in either house 2 or 3. If he were in house 4, there's a 100% chance he's in house 3. We can visualize this as follows:


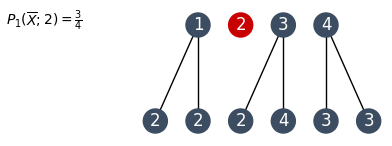
Seeing that it is more probable that the robber is now in house 2, let's be greedy and guess house 2 this time. Three out of the six possible houses are house 2, so there's a 50% chance that we make a wrong guess $(P_2(\overline{X}, 3) = \frac{3}{6}$.


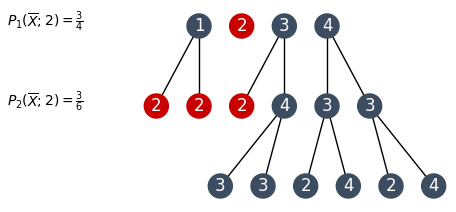
If we continue with this greedy approach (whenever possible), we'll end up with an success rate of about 94% ($1 - \frac{3}{4} \cdot \frac{3}{6} \cdot \frac{4}{6} \cdot \frac{2}{8} = 0.9375$).


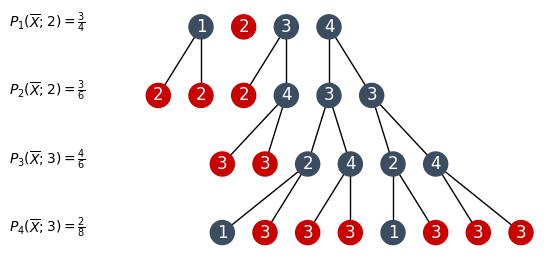
Is this best we can do? Not quite: The sequence 2, 3, 2, 2 gives a success rate of 100%.


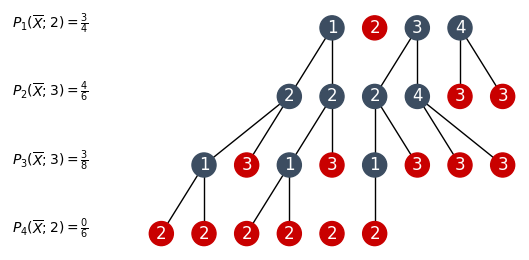
Clearly, a greedy approach won't do. We have to modify our algorithm to explore all possible guesses before making a guess and pick the one with the minimum probability of being a wrong guess. For this, we can write a depth-first search as follows.

```
def dfs(houses, level=0, arr_min=1, arr_max=8):
if level == arr_max - 1:
most_common = Counter(houses).most_common(1)[0][0]
prob = 1 - houses.count(most_common) / len(houses)
return [most_common], prob

uniq_houses = list(set(houses))
probs = []

for house in uniq_houses:
if level == 0:
print(house)
prob = 1 - houses.count(house) / len(houses)

next_houses = []
for i in houses:
if i == house: continue
if i != arr_min:
next_houses.append(i - 1)
else:
next_houses.append(i + 1)
if i != arr_max:
next_houses.append(i + 1)
else:
next_houses.append(i - 1)

_next_houses, next_prob = dfs(next_houses,
level=level + 1,
arr_min=arr_min,
arr_max=arr_max)
probs.append(([house] + _next_houses, prob * next_prob))

probs = sorted(probs, key=lambda a: a[1])
return probs[0]
```

Finally, we can do a quick local simulation and verify that the our mean score over 200 trials is about 180 and our max score is close to 190. This is enough to get the flag.

```
def _simulate(start):
if randint(0, 1) == 0:
if start == 8:
return 7
return start + 1
if start == 1:
return 2
return start - 1

def simulate():
trials = []
for _ in range(200):
houses = []
start = randint(1, 8)
for __ in range(8):
start = _simulate(start)
houses.append(start)

trials.append(houses)
return trials

def evaluate(trial, guesses):
correct_count = 0

for houses in trial:
if 0 in [a ^ b for a, b in zip(houses, guesses)]:
correct_count += 1

return correct_count

guesses, probs = dfs(houses)

samples = []
for _ in range(1000):
trials = simulate()
samples.append(evaluate(trials, guesses))

print(f'Mean: sum(samples) / len(samples)')
print(f'Max: max(samples)')
```

[Here's ](https://github.com/gov-ind/ctf_solves/raw/main/2022/hsctf/tunnels/solve.py)the full solve script.

Original writeup (https://gov-ind.github.io/hsctf_2022).