Tags: rsa
Rating: 5.0
Let's see what values we an get from the private key PEM file.
```console
$ openssl asn1parse -in corrupted-priv.pem
0:d=0 hl=4 l=1187 cons: SEQUENCE
4:d=1 hl=2 l= 1 prim: INTEGER :00
7:d=1 hl=4 l= 257 prim: INTEGER :C91C0D55929BB90511C071DE32A9ACAAC27FE205A0604DB9F5FA6B9FF99226F7487A9D7E1414BA7B46D948DEE09B90BF10DB430B12F453298D70E786C5342916BC4DDB05D4117720E4334C5DC17B155E8F7CFFA17F47248CD900FCCE7FEAB9549400F2484C3CD2EFF0300374FC412B5E428A904361FC2C33200F0CA4E99A79CE481E0F0EBE16CB42517C4CB6851FE1FA05B11678EA232F71ECC3ED5E8BEF6E3DC642C4F7488F0C5296284C4FFD1AFD1BCAC024192870AE6C5647DAB7BF71C350483180B08161A48E716788CC3CECEF26F25355C8028E7D24557CFC0F7F11633D0E4B2B2EA8DB2CCBEFBE5F424938554F24B618421A834798F2CB9DCDAA3E37B1
268:d=1 hl=2 l= 3 prim: INTEGER :01AAAA
273:d=1 hl=4 l= 256 prim: INTEGER :6D03966D15A6245F35A720E3C8FD3C87552465C28C2E609924A08D6AC39BFE67F07736CB69D76EAFF93D465E85CCF67089FF4B531D1B602736555277077C137EBF0BD6AADC627429D8E177A83602B07172D644354E90FDA1536A0F0F5F3A5DF77CB45670BEC6C8EAA3D3B9768DDCBC15C26DC417375EF0706AD98A1BE4AD0F4036B44CD7CEE21C57FF6CC8ABC343AB2AC9531754E2E6BC4E5E2481DEA6345EEDCFAD068DDE83420C49CB30267924062DAD26250473ED2606144F6FA437483636098BD14EFB4EC9E27E7A58224AE58475C365114D9A8F90CAD18C44C75DCC92FF64858AAA9EC037FA298EEA93A8775470E3330EC3E29F74B1879E836D5518090B
533:d=1 hl=3 l= 129 prim: INTEGER :F338F9C19E2D2F1715232E3121FD0A3615B9C6F87757A59BB8C507185BA7CDDE90F4DB7B49D4B0A8AD6E492C49E5D3D75FD61ED27C6D714D68D4330596CC08222CC8B641DF4ACF02D9A9D2A1115CDACC1FC2DFFC56308BCCCC4FCBC64CCE95F991C65DE43F56B67F74F7D2877AF7191B97783226B4F2C5E2AB8B67CBE0162BEB
665:d=1 hl=3 l= 129 prim: INTEGER :D3ACB64C7F034F4DA31EFC3A1FE6C86AA6536246897D081B4446BEB2A66970EF66962757ED3016E463CCD7077F35347A2AEE37E5B8C2290AA97CC7E1BC84BCECBEF25FFF7C5AF30870E6850100B032BBA6E51C1BFF4CAEB5FDEE46D9DADF1A558E8DAAABAD5191A4EC7929DA109139B7437C36A5B6E911D4EA60E236EB1FCFD3
797:d=1 hl=3 l= 128 prim: INTEGER :5B98F6777A0D7792CEEF8B3E8971303E09F826115AE81C9BEDBD2DCBB57BB948F21FD50F4C47205BF7FA30566B19E1F86F6E73B42A956869E31A3295C8CED6E9F0EF9BCB94B26AFBD8996BAF1F3DD506F0DD0CD3819EE89F0303256FDB217BD5979B72CEBE00896413C4BDBE561FD22B909892CFB6047ADE3F7F697688970FFD
928:d=1 hl=3 l= 128 prim: INTEGER :23DDF496B79B578A0D1E56BAE6FF17D10DF1C62C9D5FCD5283235CC12DED626EE2DD367CB1D53C3803ADA5B9E7823536FC9AB40993A9E97E5B0257D1ED8EAD92ED88155046205711A6FD6B228AF7E103F3EFBD09742544C02D448E46CC6BE7EFDF65A3B43A7718EC41AF4BA500B886A8DCEC3EA03572DB8485AA07CF22F1B8D5
1059:d=1 hl=3 l= 129 prim: INTEGER :B5FE419C7585A617DC2FCED225EAABA4345C3E69CE33823694B1A2FF498A13DA3BD5A3061DD665912149D10E2F08F2199BC1F8B4D62716C6C38BFD16907E6D9F5870A7F19BC3922157C3F60ABCF16AA83248A087A33664E7C91E1398C6EDC85587573C599788E30606F8A5C9706119C3CCEC8EC732A67683F856A414DCAC1C43
```
Below is a reference image so we know what we're looking at.
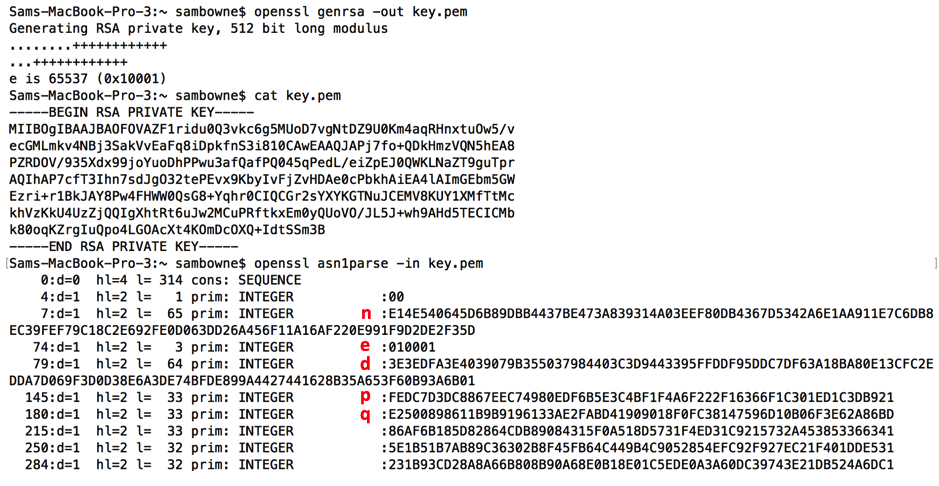
<em>https://samsclass.info/141/proj/pCH-RKF.htm</em>
We can see that we have `n`,`p`,`q`,`d`, but `e` has been corrupted with A's (We know `e` is corrupted because 01AAAA = 109226, which is not coprime with phi. You can also check this by actually trying to decrypt the message with this key and it will fail.). We have enough information to know that `e` must fall between 0x010000 and 0x01AAAA (65536 and 109226) because it's a 3-byte integer starting with `01`. Now we just need to brute force values of `e` until we successfully decrypt the message.
IF YOU KNOW RSA WELL, YOU CAN ALSO CALCULATE `e = modinv(d, totient(p,q))`
Let's first turn the encrypted file into base64:
`cat encryptedmessage.enc| base64 > b64-msg.enc`
The python script I used creates a private key for each value of e, and then tries to decrypt the message. I did this instead of normal RSA decyryption of `c^d mod N` because the `openssl rsautl` command used to encrypt the message adds padding and some randomness. Decryption with a keyfile will deal with this, but normal decryption won't. If there is a better method, please let me know, I am still a crypto n00b.
```python
import base64
from Crypto.Util.number import *
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_v1_5
ct = open('b64-msg.enc', 'r')
m = ct.read()
message_bytes = base64.b64decode(m)
p = 170796690670149105967813113382240505264948946083779586225654103308455488484955325942435054455489163709901661752475987135208117710882465445438716967370656724411467295069033290926317928181839183115857695607269318815355418951302758625104112455758674321597170318312608293648437083737653529431390940141417376656363
q = 148642998867368974873367801833129614874516289477879330501274056446035580016863921172640657206956948700028292330318518525531134043765361989080527137024999373411614110609856551202314420763429763536035853618803223901065359478539557924348825167340722079773893879969151857740258435351842073683199730747819312533459
n = 25387732297833342716406365438130607978804542306713947924435331278825835613966364990877878071229218390336047947394893275824021245301540279031050549259685735429097321770860683715441415572145285171511058018471832240316919219325571839407646640525576111529175326060738323820627674790917627092281593777378667296455593462425686619072211587683286381106745677410346749548206189587847698790256739621004469124266252563975862105678424182398082619047718005077167924092717801910113691917127487467000529529894013918559272868470229847942439455145215839736591429713580198376354923777237592764403089323518325962809234896611415982749617
phi = (p-1)*(q-1)
for e in range(65536, 109226):
# make sure e is a valid RSA public exponent (coprime with phi) or else the RSA construct will fail
if GCD(e, phi) == 1:
# get decryption key
d = inverse(e, phi)
# create private key
privkey = RSA.construct((n, e, d, p, q))
key = PKCS1_v1_5.new(privkey)
try:
# attempt to decrypt message with current privkey
pt = key.decrypt(message_bytes, "").decode()
print(f"e: {e}")
print(f"Plaintext: {pt}")
break
except:
pass
```
Output:
```console
e: 79631
Plaintext: PCTF{g1mm3_th3_e}
```
This took my VM about 2 minutes to finish, so not that bad.